副标题#e#
08年9月入学,12年7月毕业,结束了我在软件学院愉快丰富的大学生活。此系列是对四年专业课程学习的回顾,索引参见:http://www.voidcn.com/article/p-srsfcefa-vo.html
?
二叉树
二叉树是每个结点最多有两个子树的有序树。通常子树的根被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。

二叉树有几点重要的性质:
- ?性质1:在二叉树的第 i 层上至多有2i-1 个结点。 (i≥1)
- 性质2:深度为 k 的二叉树上至多含2k-1 个结点(k≥1)。
- 性质3:对任何一棵二叉树,若它含有n0 个叶子结点、n2 个度为 2 的结点,则必存在关系式:n0 = n2+1。
- 性质4:具有 n 个结点的完全二叉树的深度为log2n+1
- 性质5:若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号,则对完全二叉树中任意一个编号为 i 的结点:
(1) 若 i=1,则该结点是二叉树的根,无双亲,否则,编号为i/2? 的结点为其双亲结点;
(2) 若 2i>n,则该结点无左孩子,否则,编号为 2i 的结点为其左孩子结点;
(3) 若 2i+1>n,则该结点无右孩子结点,否则,编号为2i+1 的结点为其右孩子结点。
采用链式存储结构实现二叉树
链式存储二叉树

?
1.首先我们要构造可以表示二叉树的节点的结构 Binary_node
2.构造类二叉树 Binary_tree,并编写其几个基本的成员函数:
Empty()-检查树是否为空;clear()-将树清空;size()-得到树的大小;leaf_count()-得到叶子数目;height()-得到树高;
以及几个重要的成员函数:
Binary_tree(const Binary_tree<Entry>&original); 拷贝构造成员函数 Binary_tree &operator=(const Binary_tree<Entry>&original);重载赋值操作符 ~Binary_tree();析构函数
?
3.分别编写遍历算法的成员函数
void inorder(void(*visit)(Entry &)); 中序遍历(LVR) void preorder(void(*visit)(Entry &)); 前序遍历(VLR) void postorder(void(*visit)(Entry &)); 后续遍历(LRV)
因为二叉树的性质,三种遍历算法我们都用递归实现,所以分别编写其递归函数
void recursive_inorder(Binary_node<Entry>*sub_root,void (*visit)(Entry &)); void recursive_preorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &)); void recursive_postorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &));
?
4.作为辅助,我们再编写一个print_tree的函数,用以以括号表示法输出
同样使用递归,编写递归函数void recursive_print(Binary_node<Entry>*sub_root);
几个重要的函数代码如下:
template<class Entry>
void Binary_tree<Entry>::inorder(void(*visit)(Entry &))
//Post: The tree has been traversed in inorder sequence
//Uses: The function recursive_inorder
{
recursive_inorder(root,visit);
}
template<class Entry>
void Binary_tree<Entry>::recursive_inorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &))
//Pre: sub_root is either NULL or points to a subtree of the Binary_tree
//Post: The subtree has been traversed in inorder sequence
//Uses: The function recursive_inorder recursively
{
if(sub_root!=NULL){
recursive_inorder(sub_root->left,visit);
(*visit)(sub_root->data);
recursive_inorder(sub_root->right,visit);
}
}
template<class Entry>
void Binary_tree<Entry>::preorder(void(*visit)(Entry &))
//Post: The tree has been traversed in preorder sequence
//Uses: The function recursive_preorder
{
recursive_preorder(root,visit);
}
template<class Entry>
void Binary_tree<Entry>::recursive_preorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &))
//Pre: sub_root is either NULL or points to a subtree of the Binary_tree
//Post: The subtree has been traversed in preorder sequence
//Uses: The function recursive_preorder recursively
{
if(sub_root!=NULL){
(*visit)(sub_root->data);
recursive_preorder(sub_root->left,visit);
recursive_preorder(sub_root->right,visit);
}
}
template<class Entry>
void Binary_tree<Entry>::postorder(void(*visit)(Entry &))
//Post: The tree has been traversed in postorder sequence
//Uses: The function recursive_postorder
{
recursive_postorder(root,visit);
}
template<class Entry>
void Binary_tree<Entry>::recursive_postorder(Binary_node<Entry>*sub_root,void(*visit)(Entry &))
//Pre: sub_root is either NULL or points to a subtree fo the Binary_tree
//Post: The subtree has been traversed in postorder sequence
//Uses: The function recursive_postorder recursively
{
if(sub_root!=NULL){
recursive_postorder(sub_root->left,visit);
recursive_postorder(sub_root->right,visit);
(*visit)(sub_root->data);
}
}
template<class Entry>
void Binary_tree<Entry>::print_tree()
{
recursive_print(root);
cout<<endl;
}
template<class Entry>
void Binary_tree<Entry>::recursive_print(Binary_node<Entry>*sub_root)
{
if(sub_root!=NULL){
cout<<sub_root->data;
cout<<"(";
recursive_print(sub_root->left);
cout<<",";
recursive_print(sub_root->right);
cout<<")";
}
}
//其他函数见源码
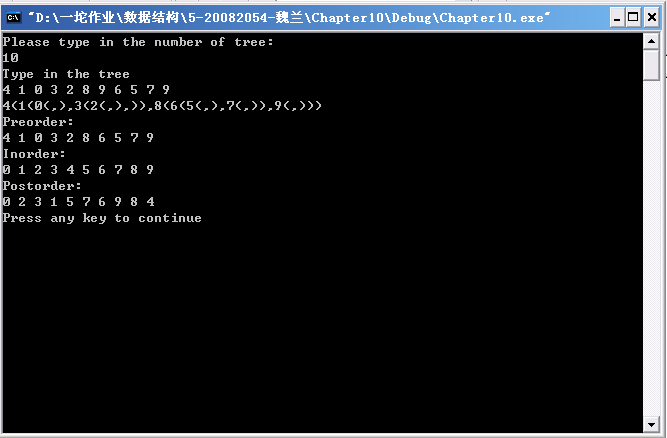
程序结果
插入二叉树并实现中序、前序和后序遍历
#p#分页标题#e#
?
AVL树
#p#副标题#e#
AVL树得名于其发明者G.M.Adelson-Velsky和E.M.Landis。AVL树是一个各结点具有平衡高度的扩展的二叉搜索树。在AVL树中,任一结点的两个子树的高度差最多为1,AVL树的高度不会超过1,AVL树既有二叉搜索树的搜索效率又可以避免二叉搜索树的最坏情况(退化树)出现。
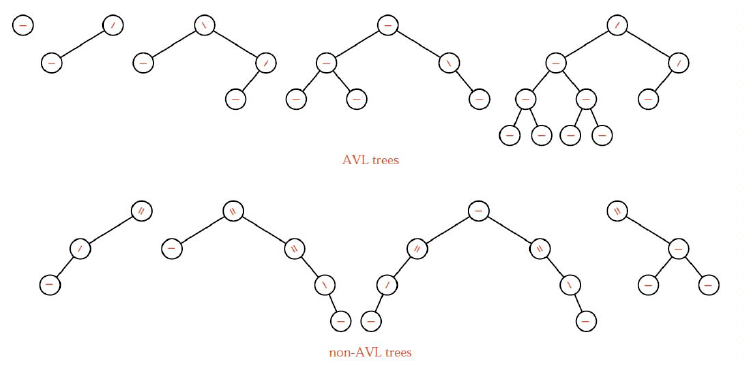
AVL树的表示与二叉搜索树类似,其操作基本相同,但插入和删除方法除外,因为它们必须不断监控结点的左右子树的相对高度,这也正是AVL树的优势所在。
实现AVL树的相关运算
1、首先我们修改结构Binary_node,增加Balance_factor用以表示节点平衡情况
2、从二叉搜索树中派生出AVL树,编写其关键的插入和删除成员函数。
Error_code insert(const Record &new_data); Error_code remove(const Record &old_data);
3、入和删除函数我们都用递归实现
编写递归函数:
Error_code avl_insert(Binary_node<Record>* &sub_root,const Record &new_data,bool &taller); Error_code avl_remove(Binary_node<Record>* &sub_root,const Record &target,bool &shorter);
以及几个重要的调用函数:
左旋右旋函数:
void rotate_left(Binary_node<Record>* &sub_root); void rotate_right(Binary_node<Record>* &sub_root);
两次旋转的左右平衡函数
void right_balance(Binary_node<Record>* &sub_root); void left_balance(Binary_node<Record>* &sub_root);
删除函数还要分别编写删除左树和删除右树的递归函数
Error_code avl_remove_right(Binary_node<Record>&sub_root,bool &shorter); Error_code avl_remove_left(Binary_node<Record>*&sub_root,bool &shorter);
?
4、个重要的成员函数代码如下:
template<class Record>
Error_code AVL_tree<Record>::insert(const Record &new_data)
//Post: If the key of new_data is already in the AVL_tree,a code of duplicate_error
// is returned. Otherwise,a code of success is returned and the Record
// new_data is inserted into the tree in such a way that the properties of an
// AVL tree are preserved.
{
bool taller;
return avl_insert(root,new_data,taller);
}
template<class Record>
Error_code AVL_tree<Record>::avl_insert(Binary_node<Record>* &sub_root,bool &taller)
//Pre: sub_root is either NULL or points to a subtree of the AVL tree
//Post: If the key of new_data is already in the subtree,a code of success is returned and the Record
// new_data is inserted into the subtree in such a way that the properties of
// an AVL tree have been preserved. If the subtree is increase in height,the
// parameter taller is set to true; otherwise it is set to false
//Uses: Methods of struct AVL_node; functions avl_insert recursively,left_balance,and right_balance
{
Error_code result=success;
if(sub_root==NULL){
sub_root=new Binary_node<Record>(new_data);
taller=true;
}
else if(new_data==sub_root->data){
result=duplicate_error;
taller=false;
}
else if(new_data<sub_root->data){//Insert in left subtree
result=avl_insert(sub_root->left,taller);
if(taller==true)
switch(sub_root->get_balance()){//Change balance factors
case left_higher:
left_balance(sub_root);
taller=false;
break;
case equal_height:
sub_root->set_balance(left_higher);
break;
case right_higher:
sub_root->set_balance(equal_height);
taller=false;
break;
}
}
else{ //Insert in right subtree
result=avl_insert(sub_root->right,taller);
if(taller==true)
switch(sub_root->get_balance()){
case left_higher:
sub_root->set_balance(equal_height);
taller=false;
break;
case equal_height:
sub_root->set_balance(right_higher);
break;
case right_higher:
right_balance(sub_root);
taller=false; //Rebalancing always shortens the tree
break;
}
}
return result;
}
template<class Record>
void AVL_tree<Record>::right_balance(Binary_node<Record>* &sub_root)
//Pre: sub_root points to a subtree of an AVL_tree that is doubly unbalanced
// on the right
//Post: The AVL properties have been restored to the subtree
{
Binary_node<Record>* &right_tree=sub_root->right;
switch(right_tree->get_balance()){
case right_higher:
sub_root->set_balance(equal_height);
right_tree->set_balance(equal_height);
rotate_left(sub_root);
break;
case equal_height:
cout<<"WARNING: program error detected in right_balance "<<endl;
case left_higher:
Binary_node<Record>*sub_tree=right_tree->left;
switch(sub_tree->get_balance()){
case equal_height:
sub_root->set_balance(equal_height);
right_tree->set_balance(equal_height);
break;
case left_higher:
sub_root->set_balance(equal_height);
right_tree->set_balance(right_higher);
case right_higher:
sub_root->set_balance(left_higher);
right_tree->set_balance(equal_height);
break;
}
sub_tree->set_balance(equal_height);
rotate_right(right_tree);
rotate_left(sub_root);
break;
}
}
template<class Record>
void AVL_tree<Record>::left_balance(Binary_node<Record>* &sub_root)
{
Binary_node<Record>* &left_tree=sub_root->left;
switch(left_tree->get_balance()){
case left_higher:
sub_root->set_balance(equal_height);
left_tree->set_balance(equal_height);
rotate_right(sub_root);
break;
case equal_height:
cout<<"WARNING: program error detected in left_balance"<<endl;
case right_higher:
Binary_node<Record>*sub_tree=left_tree->right;
switch(sub_tree->get_balance()){
case equal_height:
sub_root->set_balance(equal_height);
left_tree->set_balance(equal_height);
break;
case right_higher:
sub_root->set_balance(equal_height);
left_tree->set_balance(left_higher);
break;
case left_higher:
sub_root->set_balance(right_higher);
left_tree->set_balance(equal_height);
break;
}
sub_tree->set_balance(equal_height);
rotate_left(left_tree);
rotate_right(sub_root);
break;
}
}
template<class Record>
void AVL_tree<Record>::rotate_left(Binary_node<Record>* &sub_root)
//Pre: sub_root points to a subtree of the AVL_tree. This subtree has
// a nonempty right subtree.
//Post: sub_root is reset to point to its former right child,and the
// former sub_root node is the left child of the new sub_root node
{
if(sub_root==NULL||sub_root->right==NULL)//impossible cases
cout<<"WARNING: program error detected in rotate_left"<<endl;
else{
Binary_node<Record>*right_tree=sub_root->right;
sub_root->right=right_tree->left;
right_tree->left=sub_root;
sub_root=right_tree;
}
}
template<class Record>
void AVL_tree<Record>::rotate_right(Binary_node<Record>*&sub_root)
{
if(sub_root==NULL||sub_root->left==NULL)
cout<<"WARNING:program error in detected in rotate_right"<<endl;
else{
Binary_node<Record>*left_tree=sub_root->left;
sub_root->left=left_tree->right;
left_tree->right=sub_root;
sub_root=left_tree;
}
}
template<class Record>
Error_code AVL_tree<Record>::remove(const Record &old_data)
{
bool shorter;
return avl_remove(root,old_data,shorter);
}
template<class Record>
Error_code AVL_tree<Record>::avl_remove(Binary_node<Record>* &sub_root,bool &shorter)
{
Binary_node<Record>*temp;
if(sub_root==NULL)return fail;
else if(target<sub_root->data)
return avl_remove_left(sub_root,target,shorter);
else if(target>sub_root->data)
return avl_remove_right(sub_root,shorter);
else if(sub_root->left==NULL){//Found target: delete current node
temp=sub_root; //Move right subtree up to delete node
sub_root=sub_root->right;
delete temp;
shorter=true;
}
else if(sub_root->right==NULL){
temp=sub_root; //Move left subtree up to delete node
sub_root=sub_root->left;
delete temp;
shorter=true;
}
else if(sub_root->get_balance()==left_higher){
//Neither subtree is empty; delete from the taller
temp=sub_root->left;//Find predecessor of target and delete if from left tree
while(temp->right!=NULL)temp=temp->right;
sub_root->data=temp->data;
avl_remove_left(sub_root,temp->data,shorter);
}
else{
temp=sub_root->right;
while(temp->left!=NULL)temp=temp->left;
sub_root->data=temp->data;
avl_remove_right(sub_root,shorter);
}
return success;
}
template<class Record>
Error_code AVL_tree<Record>::avl_remove_right(Binary_node<Record>
*&sub_root,bool &shorter)
{
Error_code result=avl_remove(sub_root->right,shorter);
if(shorter==true)switch(sub_root->get_balance()){
case equal_height:
sub_root->set_balance(left_higher);
shorter=false;
break;
case right_higher:
sub_root->set_balance(equal_height);
break;
case left_higher:
Binary_node<Record>*temp=sub_root->left;
switch(temp->get_balance()){
case equal_height:
temp->set_balance(right_higher);
rotate_right(sub_root);
shorter=false;
break;
case left_higher:
sub_root->set_balance(equal_height);
temp->set_balance(equal_height);
rotate_right(sub_root);
break;
case right_higher:
Binary_node<Record>*temp_right=temp->right;
switch(temp_right->get_balance()){
case equal_height:
sub_root->set_balance(equal_height);
temp->set_balance(equal_height);
break;
case left_higher:
sub_root->set_balance(right_higher);
temp->set_balance(equal_height);
break;
case right_higher:
sub_root->set_balance(equal_height);
temp->set_balance(left_higher);
break;
}
temp_right->set_balance(equal_height);
rotate_left(sub_root->left);
rotate_right(sub_root);
break;
}
}
return result;
}
template<class Record>
Error_code AVL_tree<Record>::avl_remove_left(Binary_node<Record>
*&sub_root,bool &shorter)
{
Error_code result=avl_remove(sub_root->left,shorter);
if(shorter==true)
switch(sub_root->get_balance()){
case equal_height:
sub_root->set_balance(right_higher);
shorter=false;
break;
case left_higher:
sub_root->set_balance(equal_height);
break;
case right_higher:
Binary_node<Record>*temp=sub_root->right;
switch(temp->get_balance()){
case equal_height:
temp->set_balance(left_higher);
rotate_right(sub_root);
shorter=false;
break;
case right_higher:
sub_root->set_balance(equal_height);
temp->set_balance(equal_height);
rotate_left(sub_root);
break;
case left_higher:
Binary_node<Record>*temp_left=temp->left;
switch(temp_left->get_balance()){
case equal_height:
sub_root->set_balance(equal_height);
temp->set_balance(equal_height);
break;
case right_higher:
sub_root->set_balance(left_higher);
temp->set_balance(equal_height);
break;
case left_higher:
sub_root->set_balance(equal_height);
temp->set_balance(right_higher);
break;
}
temp_left->set_balance(equal_height);
rotate_right(sub_root->right);
rotate_left(sub_root);
break;
}
}
return result;
}
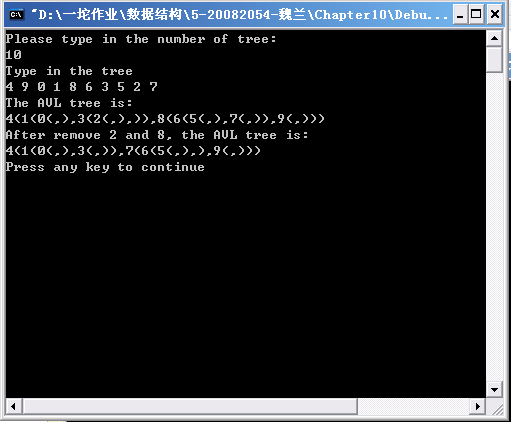
实验结果
#p#副标题#e##p#分页标题#e#
实现如下功能:1)由{4,9,1,8,6,3,5,2,7}建AVL树B,并以括号表示法输出;2)删除B中关键字为8和2的结点,输出结果。
?
分析总结
#p#副标题#e##p#分页标题#e#
?
采用链式存储结构实现二叉树
- 二叉树在插入的时候通过判断待插入数据与根节点数据的大小,若小于根数据,插入左树,反之插入右树(我们规定不许有重复元素);二叉树的存储结构常用于搜索等。但搜索的效率常依赖于树的结构。而树的结构与元素插入顺序有很大关系,用上述方法插入时若插入的元素是有序的,则得到的树与队列几乎没有区别,也起不到优化搜索的目的。
- 二叉树的遍历算法最为重要的一点是递归,递归使我们不必关心于具体的遍历每个节点的顺序,而只是将其看做三个部分,即左子树,根节点,右子树,具体子树的遍历仍是调用其递归函数。
3.在打印树的时候,我写的并不完美,因为对于叶子节点,理想应该不再打印括号,但我通过判断根节点不为空而调用递归函数,即只要节点有元素就会输出(,),还是表达出了树的意思,但并没有想到怎样达到简洁的效果。
实现AVL树的相关运算
- AVL树每插入,删除一个节点就会判断树的高度并改变相应节点的平衡因素,每当有节点不再满足AVL树的性质,立即通过旋转得到AVL树
- 旋转的函数及其巧妙。而插入和删除元素的函数要考虑的情况非常多,一种情况没有考虑到就可能达不到我们想要的效果,函数的编写需要极大的耐心和对编程语句的熟练掌握。很多地方我是参考书上的,别人的代码我可以理解,但我自己写可能还是会漏掉很多情况。